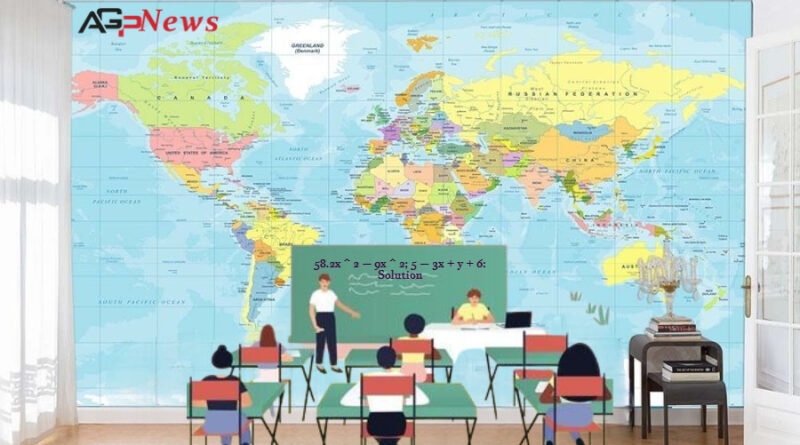
58.2x ^ 2 – 9x ^ 2; 5 – 3x + y + 6: Solution

In the intriguing realm of mathematics, equations like 58.2x^2 – 9x^2; 5 – 3x + y + 6 often present themselves as complex puzzles, inviting us to unravel their intricacies and uncover the profound insights they hold. Among these enigmatic expressions, one stands out as particularly captivating: 58.2x^2 – 9x^2; 5 – 3x + y + 6. While it may seem daunting at first glance, fear not, for we are here to guide you through its complexities, step by step.

Deciphering the Equation 58.2x^2 – 9x^2; 5 – 3x + y + 6

Let us embark on a journey of comprehension by breaking down this equation into its fundamental components and exploring their significance:

Component 1: 58.2x^2 – 9x^2

In Component 1, we encounter two distinct terms, each intertwined with the variable x raised to different powers. These terms serve as the backbone of the equation, laying the groundwork for its mathematical structure.

Component 2: 5 – 3x + y + 6

Component 2 introduces us to a quartet of terms, each contributing uniquely to the equation’s narrative. From constants like 5 and 6 to variables such as -3x and y, each element adds depth to the equation’s complexity.

With these components identified, let us delve deeper into their properties and explore the potential solutions they offer.

Analyzing the Equation 58.2x^2 – 9x^2; 5 – 3x + y + 6

To gain a comprehensive understanding of this equation, let us conduct a meticulous analysis, examining each element with precision:

Step 1: Simplifying Component 1

Within Component 1, we encounter two terms featuring x raised to the power of 2. Employing algebraic simplification, we combine these terms:

58.2x^2 – 9x^2 = 49.2x^2

Step 2: Examining Component 2

Component 2 presents a diverse array of constants and variables, each retaining its distinct identity. Further simplification proves challenging at this stage, as each element contributes uniquely to the equation’s overall composition.

Combining the Components

With our components elucidated, let us merge them to form a cohesive whole:

49.2x^2 + (5 – 3x + y + 6)

Seeking Specific Solutions

To unravel the equation’s mysteries, we must seek specific values for x and y. The outcome of the equation hinges on these input values, as they dictate the interplay of variables and constants within the expression. As it stands, the equation represents a quadratic expression, and its solution depends on the precise values assigned to x and y.

Conclusion

In conclusion, the equation 58.2x^2 – 9x^2; 5 – 3x + y + 6 embodies a profound depth of mathematical complexity. Its solution remains an enigma, contingent upon the precise input values provided for x and y. Through the intricate interplay of algebraic terms and constants, this equation underscores the importance of precision and meticulous analysis in the pursuit of mathematical solutions.

FAQs

What does the equation 58.2x^2 – 9x^2; 5 – 3x + y + 6 represent?

This equation is a mathematical expression comprising algebraic terms and constants. It presents a complex puzzle inviting exploration and analysis to understand its significance and potential solutions.

How do you simplify the components of the equation 58.2x^2 – 9x^2; 5 – 3x + y + 6?

Breaking down the equation into its constituent components, such as Component 1 (58.2x^2 – 9x^2) and Component 2 (5 – 3x + y + 6), allows for algebraic simplification and analysis to uncover its underlying structure and properties.

What is the significance of combining the components of the equation 58.2x^2 – 9x^2; 5 – 3x + y + 6?

Combining the components enables us to merge their individual narratives into a cohesive whole, facilitating a comprehensive analysis of the equation’s intricacies and potential solutions.

How do specific values for x and y impact the solution of the equation 58.2x^2 – 9x^2; 5 – 3x + y + 6?

The outcome of the equation depends on the precise input values assigned to x and y. These values dictate the interaction of variables and constants within the expression, influencing its overall solution and mathematical significance.

What insights does the equation 58.2x^2 – 9x^2; 5 – 3x + y + 6 offer into the importance of precision in mathematical analysis?

Through its intricate interplay of algebraic terms and constants, this equation underscores the critical importance of precision and meticulous analysis in mathematical problem-solving.